- 详细介绍
- 相关信息
高分必备-11小时精通高数.下
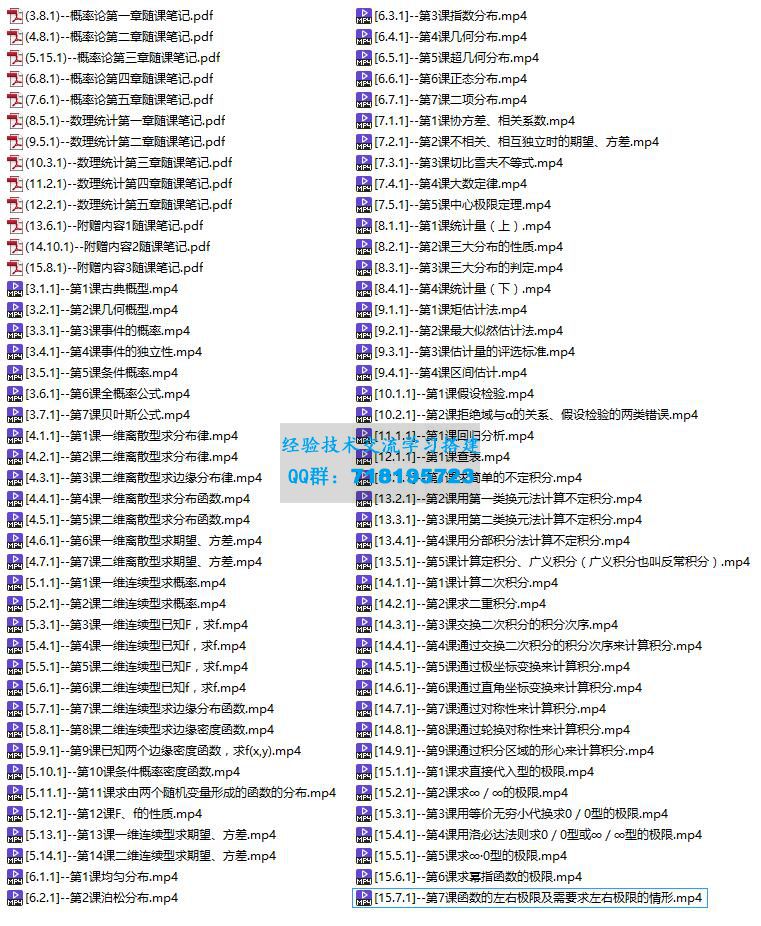
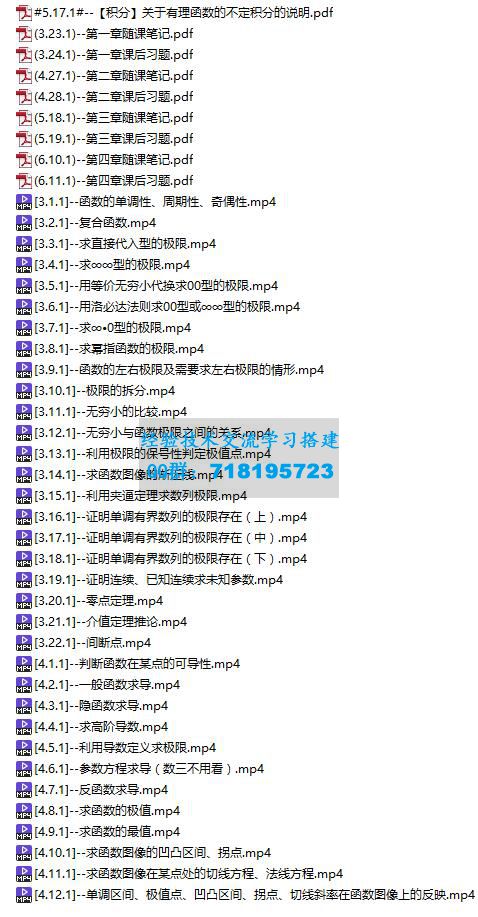
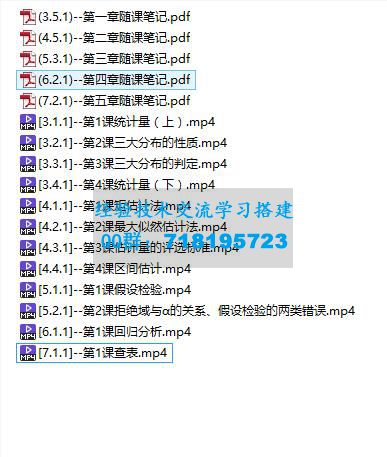
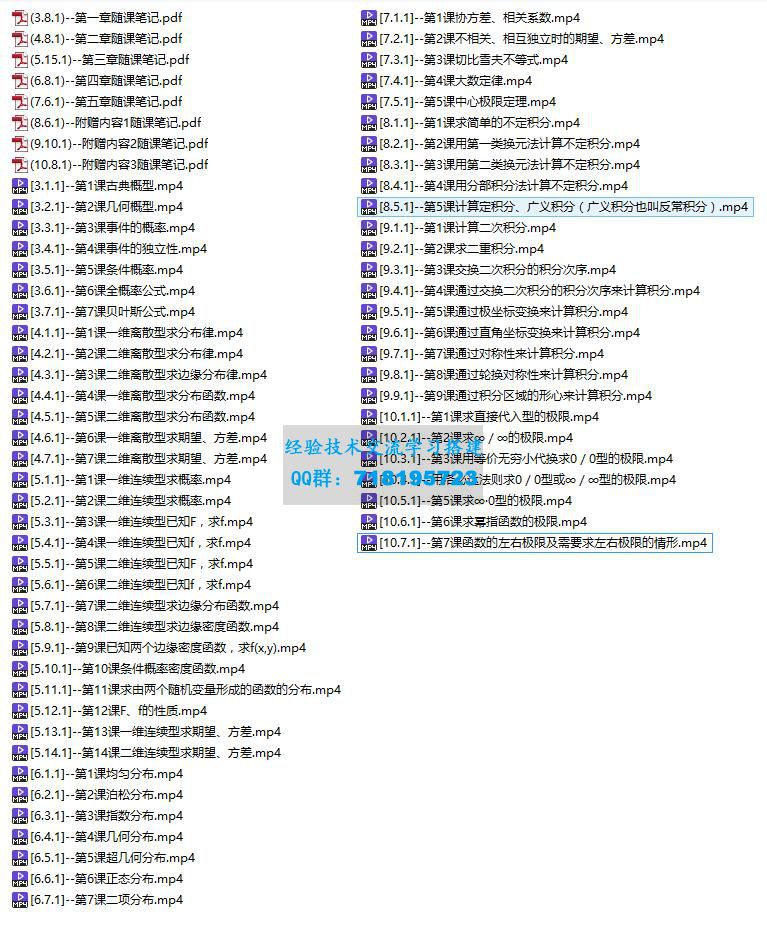
(3.21.1)--第一章随课笔记.pdf
(4.13.1)--第二章随课笔记.pdf
[3.1.1]--计算重极限.mp4
[3.10.1]--变量代换下化简偏导数满足的关系式.mp4
[3.11.1]--求全微分.mp4
[3.12.1]--已知全微分,求全微分里的未知数.mp4
[3.13.1]--判断函数在点(x0,y0)处是否可微.mp4
[3.14.1]--判断函数在点(x0,y0)处是否连续.mp4
[3.15.1]--连续、可导、可微的关系.mp4
[3.16.1]--一般函数求无条件极值.mp4
[3.17.1]--利用定义判断极值点.mp4
[3.18.1]--在约束条件下找出可能的极值点.mp4
[3.19.1]--在约束条件下求最值、最值点.mp4
[3.2.1]--证明重极限不存在.mp4
[3.20.1]--在区域上求最值、最值点.mp4
[3.3.1]--求偏导(简单情况).mp4
[3.4.1]--求偏导(复杂情况).mp4
[3.5.1]--用f′表示部分偏导.mp4
[3.6.1]--用公式法求隐函数的偏导.mp4
[3.7.1]--用两边同求偏导法求隐函数的偏导.mp4
[3.8.1]--求某点的偏导值.mp4
[3.9.1]--已知偏导数,通过积分求表达式.mp4
[4.1.1]--计算二次积分.mp4
[4.10.1]--比较二重积分的大小.mp4
[4.11.1]--二重积分中值定理.mp4
[4.12.1]--函数表达式含二重积分.mp4
[4.2.1]--求二重积分.mp4
[4.3.1]--交换二次积分的积分次序.mp4
[4.4.1]--通过交换二次积分的积分次序来计算积分.mp4
[4.5.1]--通过极坐标变换来计算积分.mp4
[4.6.1]--通过直角坐标变换来计算积分.mp4
[4.7.1]--通过对称性来计算积分.mp4
[4.8.1]--通过轮换对称性来计算积分.mp4
[4.9.1]--通过积分区域的形心来计算积分.mp4